√ 円 面積 積分 一部 206361

高校数学 定積分と面積 ２ 問題編 映像授業のtry It トライイット

解説 図のような曲線 y = f (x) と x 軸，および 2直線 x = a ，x = b で囲まれた図形の面積 S は定積分を利用して， で求められます。ここはわかっているようですね。 この を計算すると，負になってしまったのですね。 面積ですから負になるのはおかしいです。 うさぎでもわかる解析 Part27 2重積分の応用（体積・曲面積の求め方） 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめてい

円 面積 積分 一部

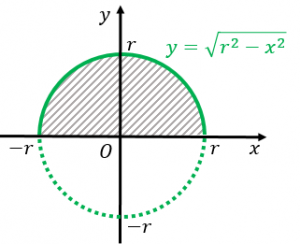
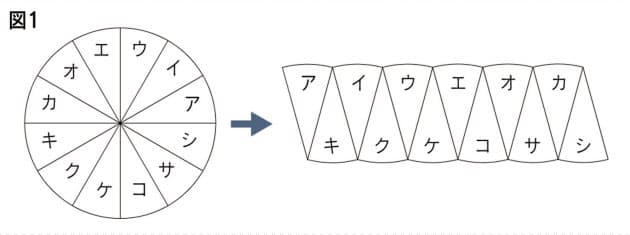
円 面積 積分 一部- 円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの これは半径3の円の上半分を表す方程式であるから,\ 本問の図形的意味は右上図の面積である どちらの解法が有利かは火を見るより明らかである {∫{a²x²}dx\ 型の定積分は,\ 必ず円の面積の一部とみて求めよう \求める定積分は,\ 右図の面積に等しい

面積の求め方 算数の教え上手 学びの場 Com

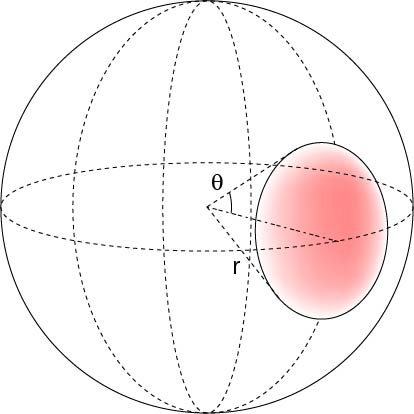
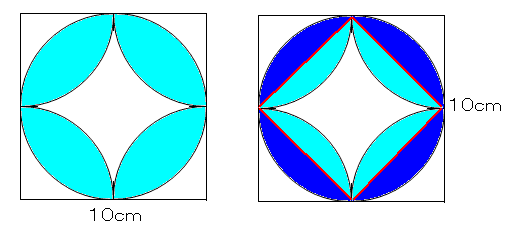
円の面積を求める公式は 円の面積 = 半径 × 半径 × 円周率 なので、半径を x とすると = x × x × 314 x × x = ÷ 314 x × x = 36 x = 6 ( c m) になります。 tweet share はてブ Pocket さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。面積と定積分の関係について，次のことが成り立ちます。 関数 \(y = f(x)\) が \(a \leqq x \leqq b\) において連続であり， \(f(x) \geqq 0\) を満たしているとき，2直線 \(x = a\) ， \(x = b\) と \(x\) 軸， \(y = f(x)\) のグラフで囲まれた図形の面積は，定積分 \(\displaystyle \int_a

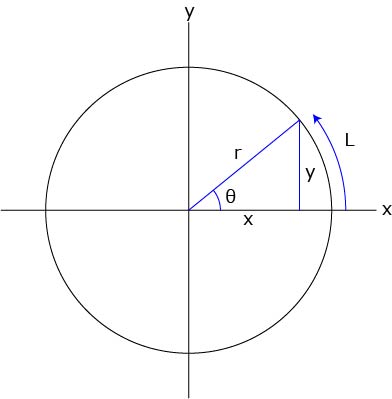
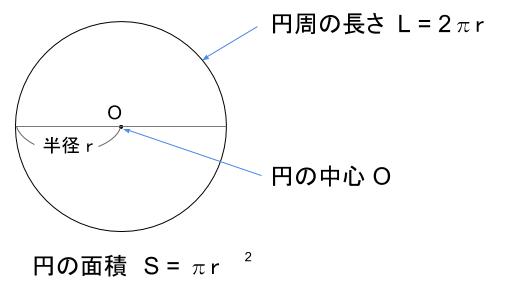
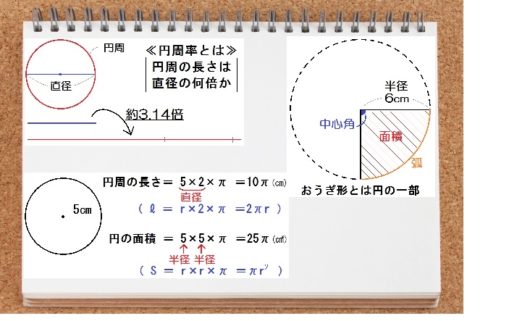
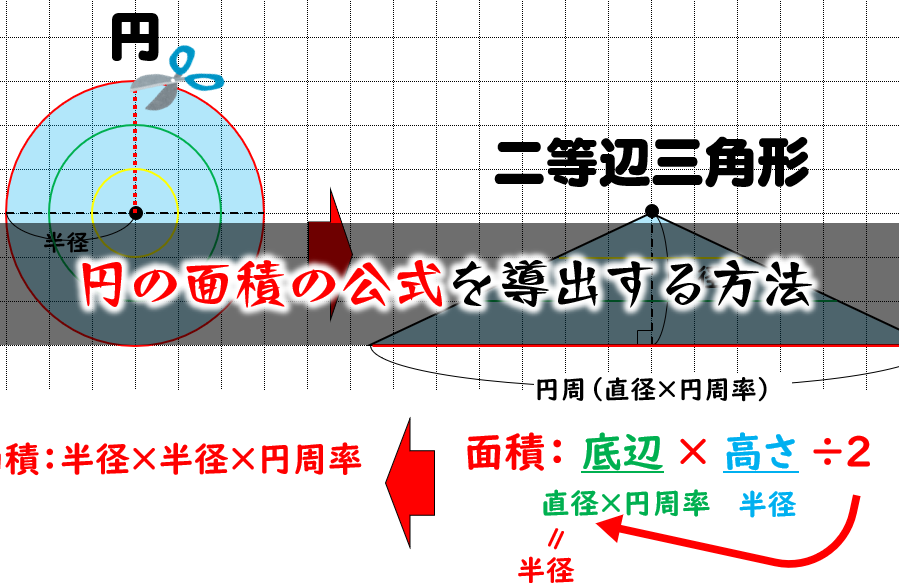
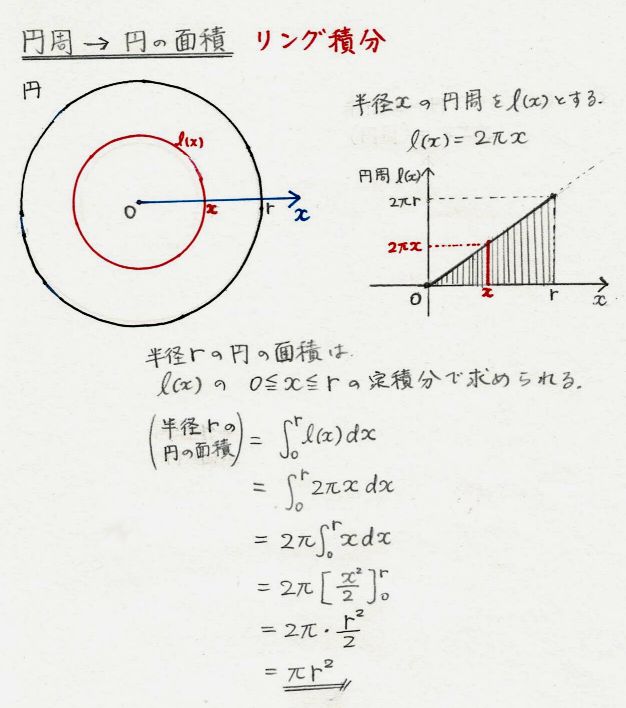
円の面積 ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ)円の面積（ S urface area） π 円周率（= 314） r 円の半径（ r adius） 公式の導き方のイメージ この円の面積を求める公式は、円を無限個の扇形に分け、それを長方形につなぎ変えることで導くことA=面積 a=面積 a=面積 もし とすれば a=面積 a=面積 もし とすれば a=面積 p=楕円の周囲 a=πab 、pを求める近似式 a=面積 a=面積bcd a=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の

円 面積 積分 一部のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法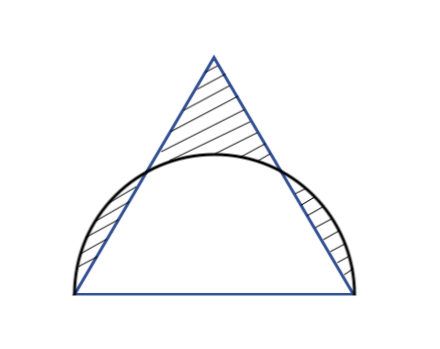
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法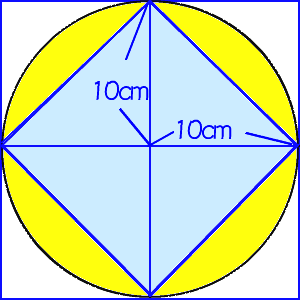
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法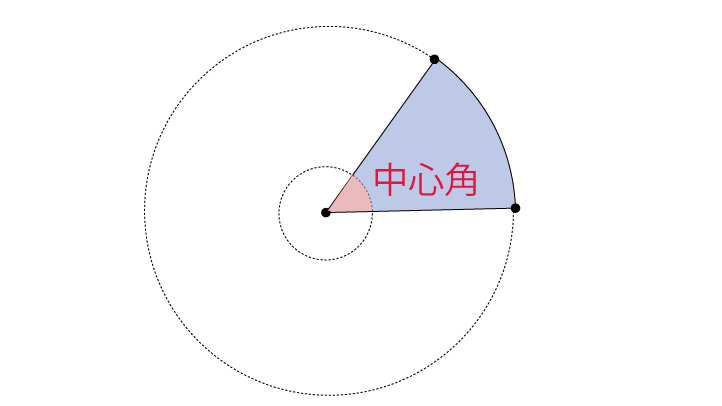
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	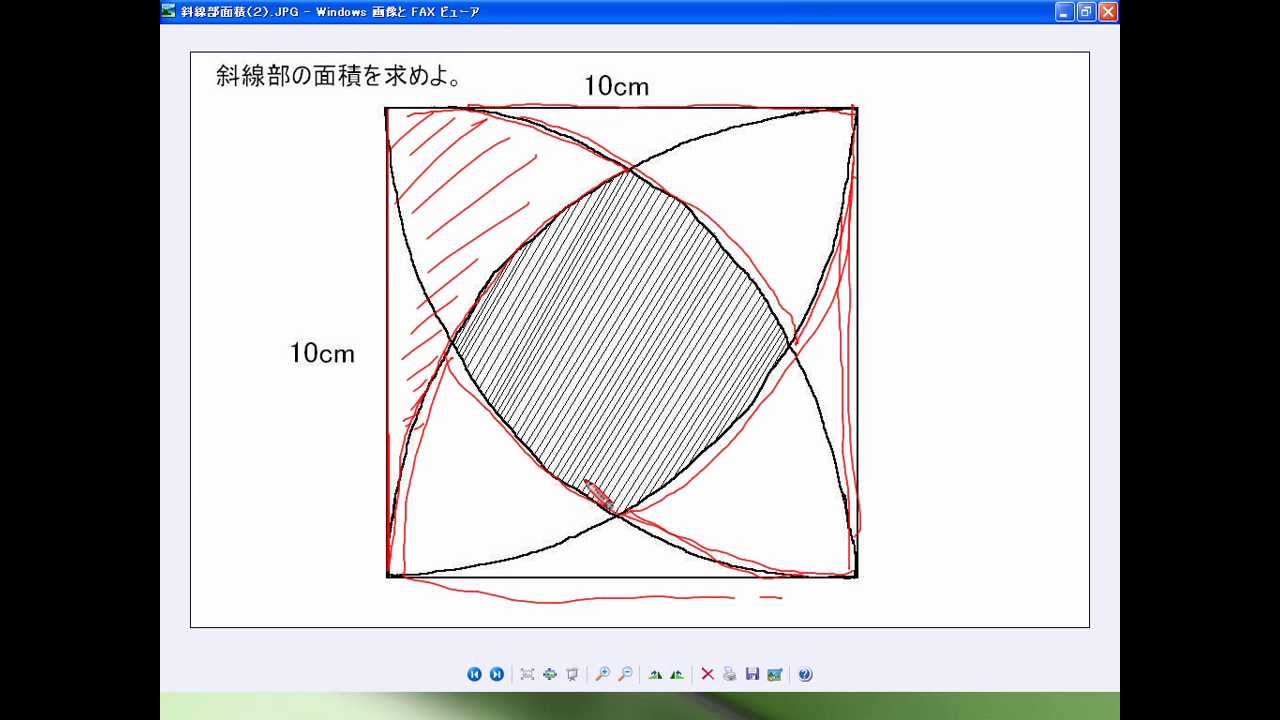欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	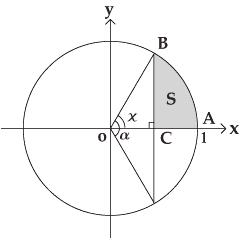欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	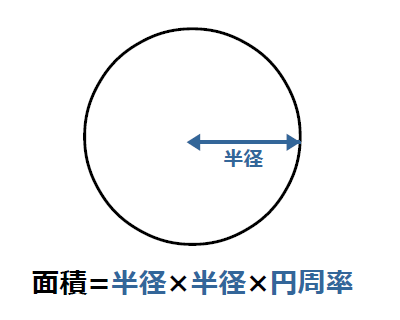欠けた円 欠円 や弓形の面積の計算方法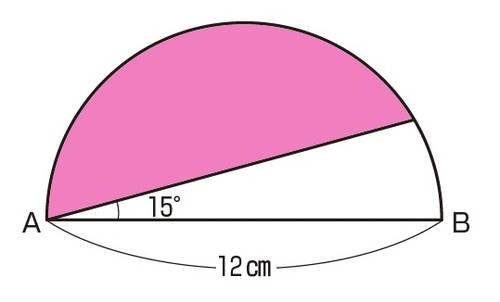
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法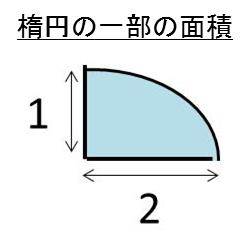
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	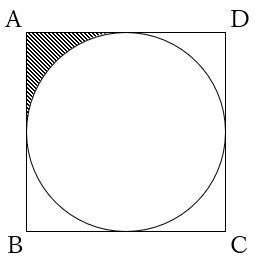欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法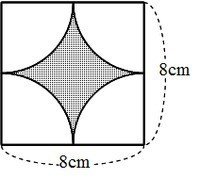
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	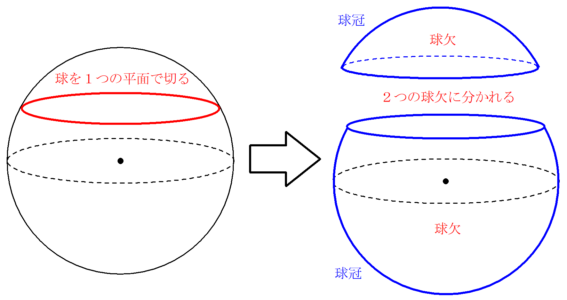欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	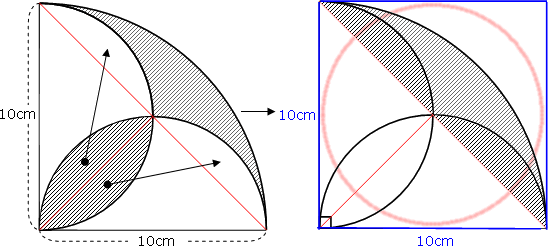欠けた円 欠円 や弓形の面積の計算方法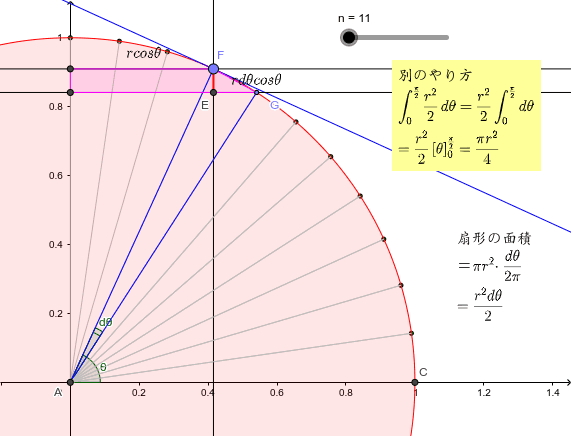
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法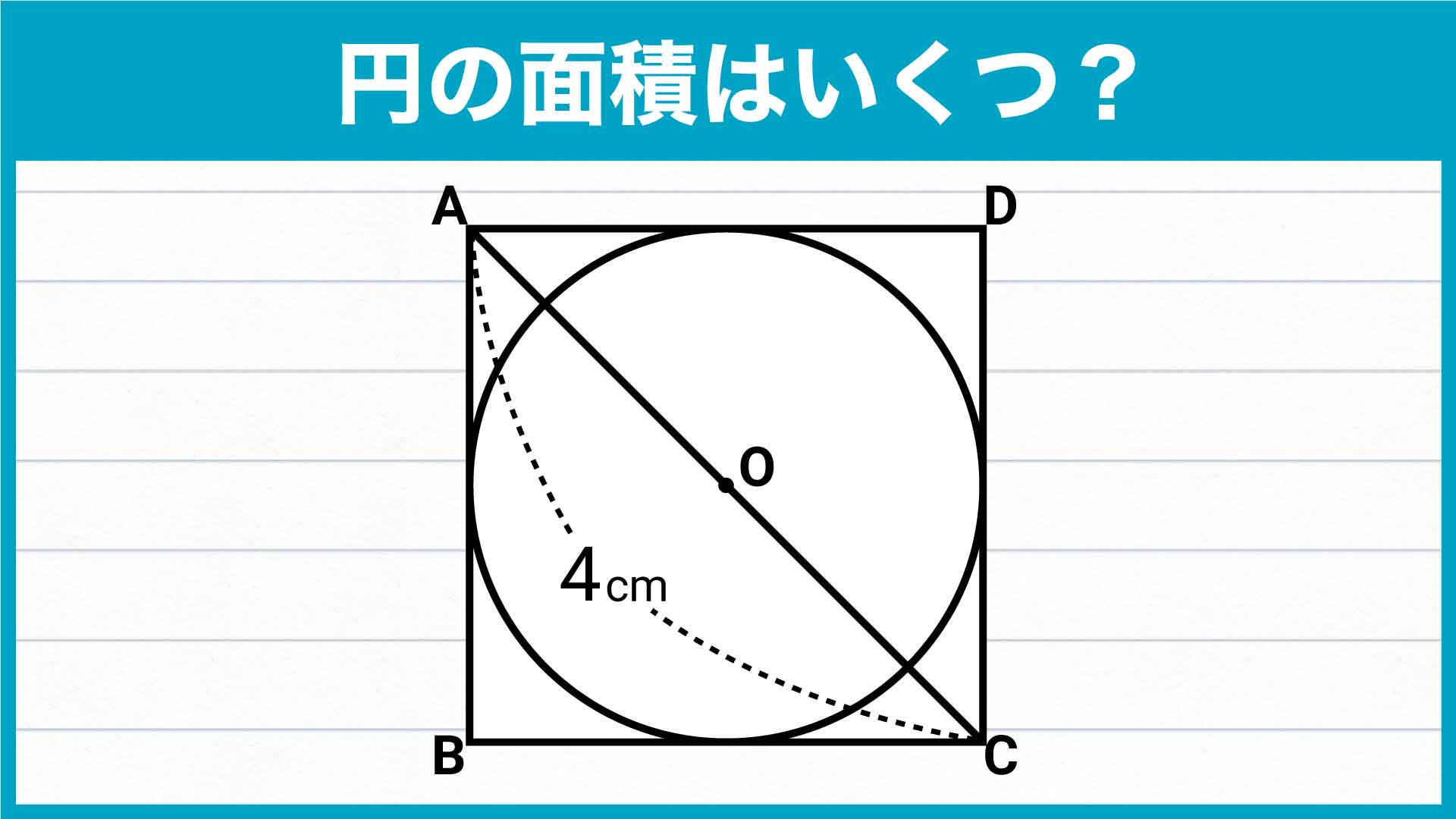
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	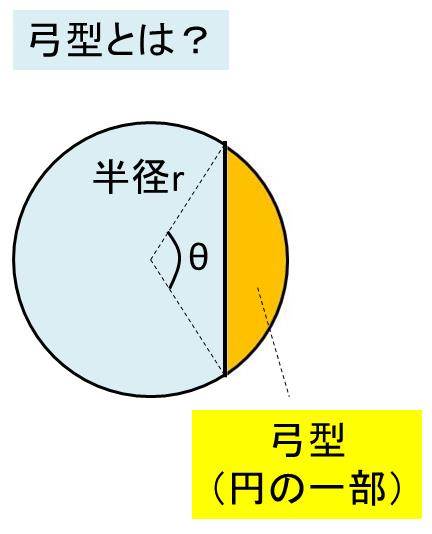欠けた円 欠円 や弓形の面積の計算方法
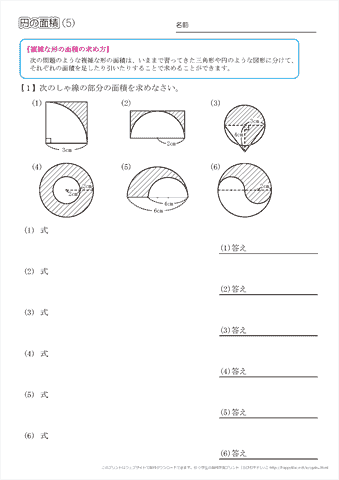欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法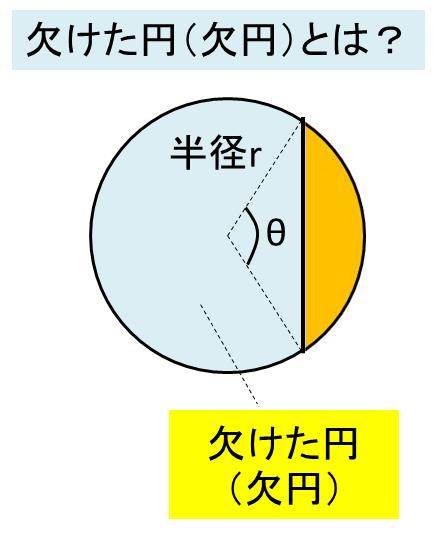
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	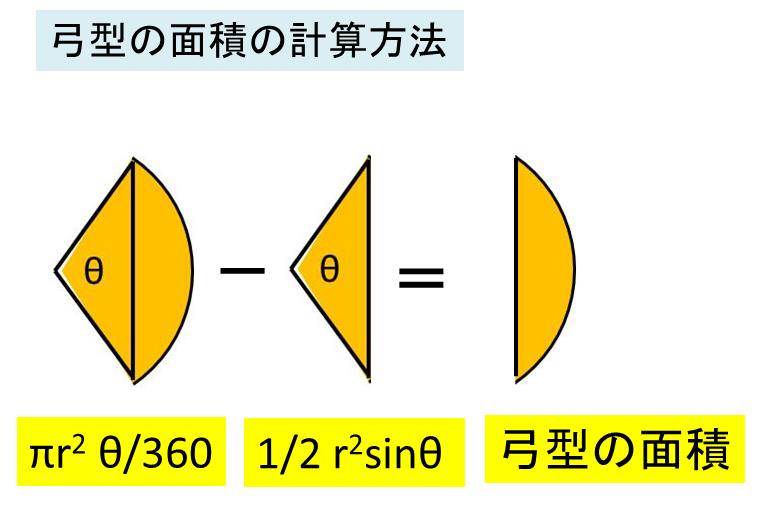欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	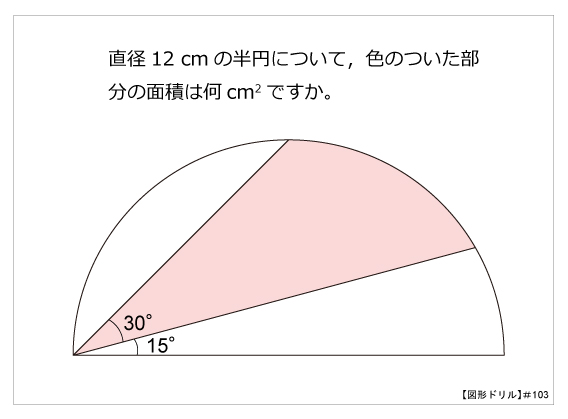欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	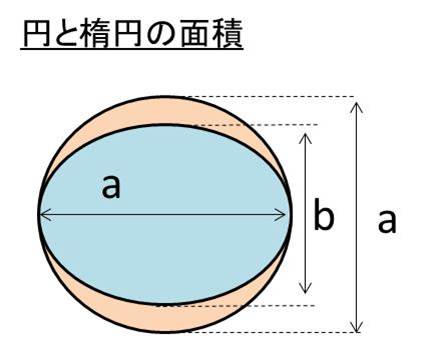欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	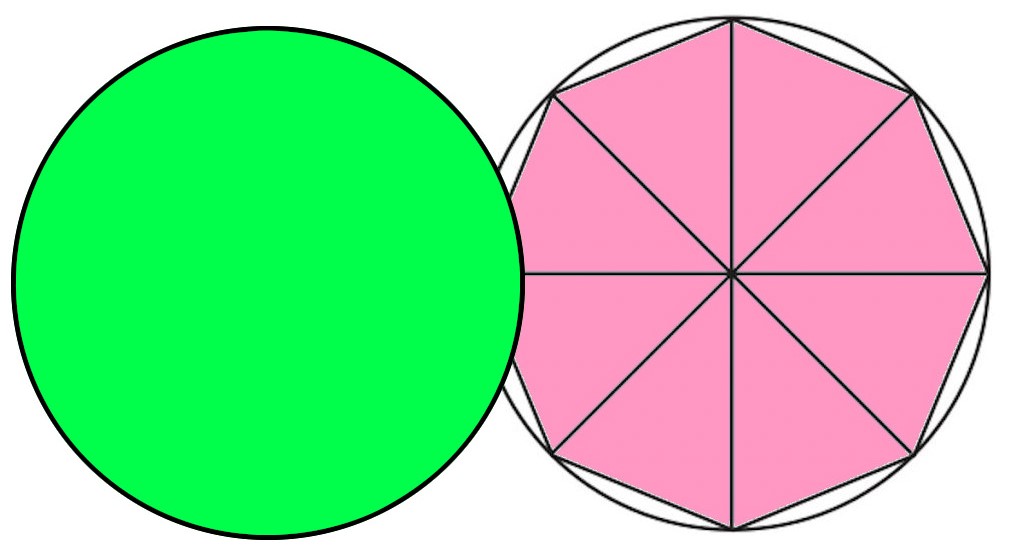欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	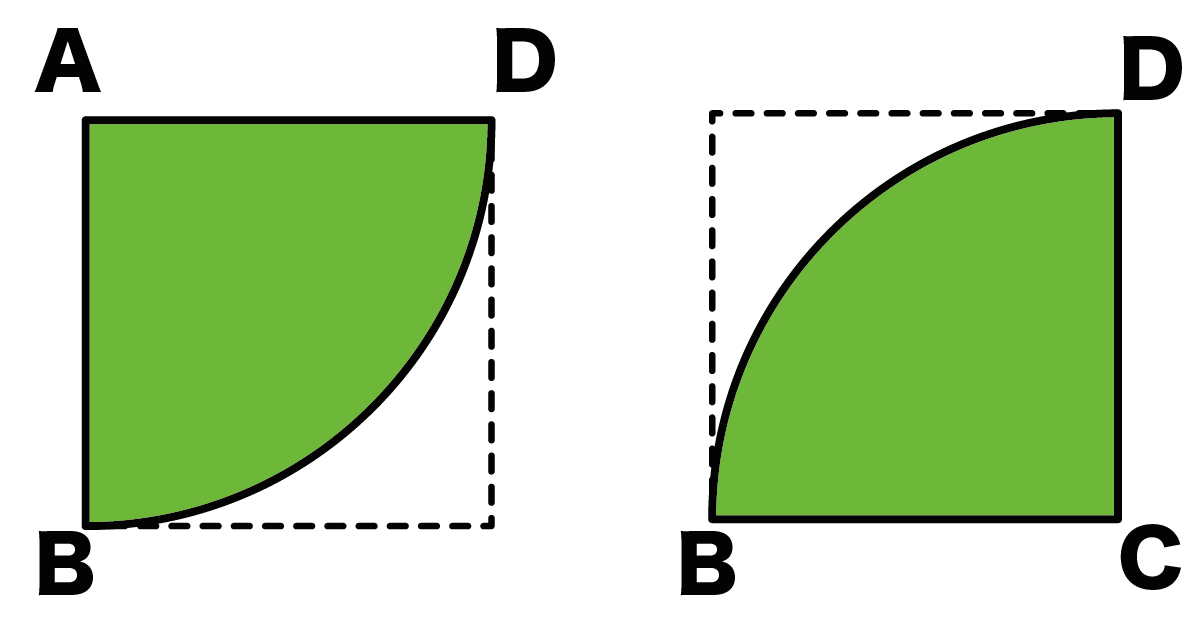欠けた円 欠円 や弓形の面積の計算方法	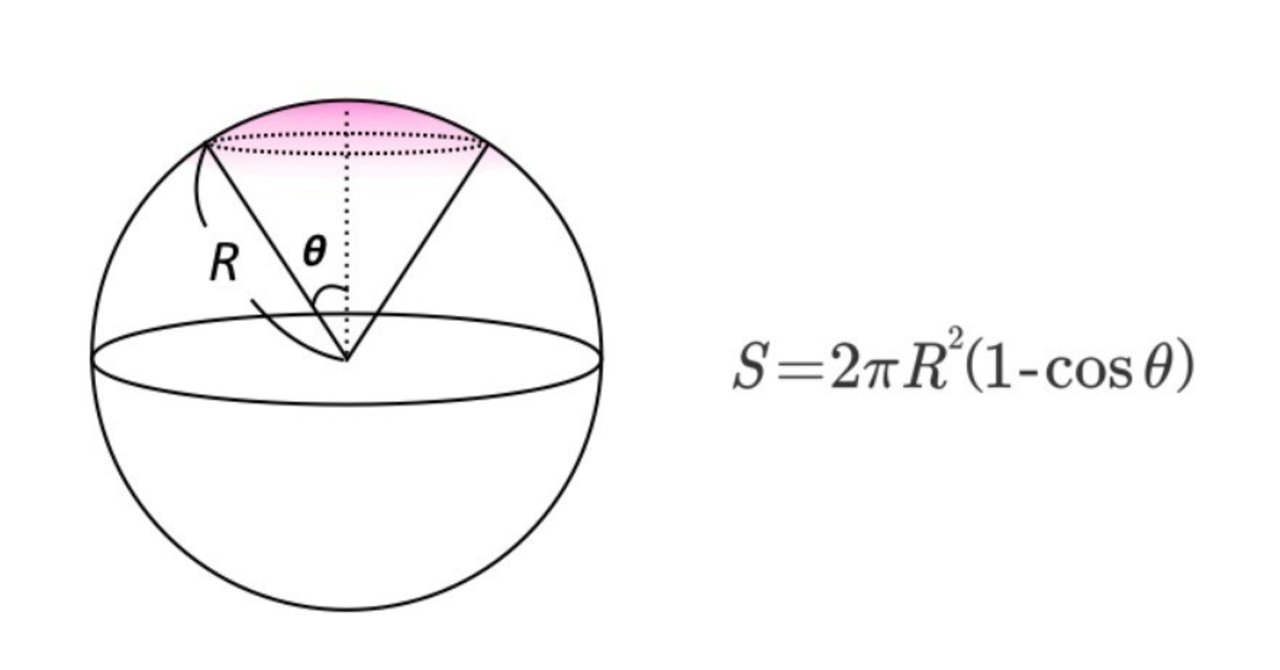欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	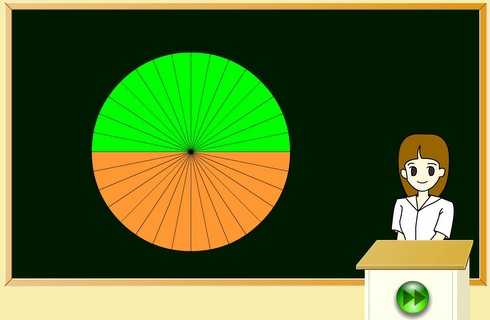欠けた円 欠円 や弓形の面積の計算方法	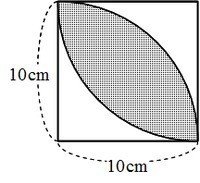欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法
欠けた円 欠円 や弓形の面積の計算方法	欠けた円 欠円 や弓形の面積の計算方法

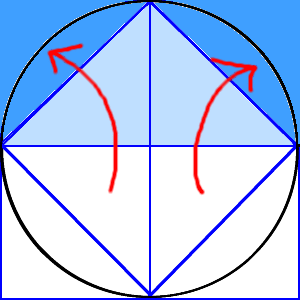
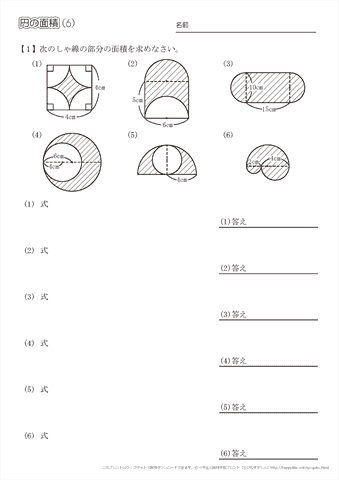
面積公式は、部分的に充填された円筒形の貯蔵タンクの体積を計算するのに用いることができる。 丸みのある天板を持つ窓やドアのデザインにおいて、 c と h だけが分かっているという場面で、製図士がコンパスで R を計算することに利用できる。採点する やり直す 解説 3 半径 10 ，中心角が90°の扇形の面積 円の面積の4分の1だから，10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ，これから三角形の面積 10×10÷2=50 を引く